经典论文讨论 A Microfacet-based BRDF Generator (2000)

内容简介

本篇文章¹主要介绍了, 在微表面元模型前提下, 已知任意法向量分布 PDF $p(\bold h)$, 计算得到满足 White Furnace Test 的 BRDF 表达式的方法. 本文的特殊之处可以体现在于下图中:

通过本文的方法可以通过计算出非常特殊的 BRDF 表达式, 使得开发者获得定制高光 Lobe 的能力, 并且也成为一种在一定假设条件下, 导出快速计算任意材质模型的方法, 其中包括绸缎, 丝绒等等材质.

重点梳理

对于任意微表面模型有:

The microfacet normals have an underlying probability density function $p(\bold h)$.

即微表面元具有 $\bold h$ 方向法向量的概率分布函数 PDF 为 $p(\bold h)$, 该 PDF 函数的另一种更为人所知的名字就是法向量分布函数 $D(\bold h)$, 即 Cook-Torrance BRDF 中的 $D$ 项.

本文简化了曲面中微表面元中的光线的遮挡效应, 假设了 $D(\bold h)$ 是不同材质 BRDF 的产生不同表现的主要因素. 只考虑了不需要射线追踪就可以获得的遮挡关系.

We believe that in most cases the shape of p(h) function itself has a much greater impact on the appearance than the shadowing. This suggests the key idea in this paper: the shadowing term should be made as simple as possible while remaining physically plausible.

As can be seen from Equation 10, at the very least shadowing should take care of the divergence at grazing angles where the denominator terms disappear: $(k_1 \cdot n)(k_2 \cdot n) → 0$.

同时, 大部分情况下, 本文都采用了非自相关的遮挡函数形式 (下面的 $P(\bold k_1, \bold k_2, \bold h)$ 表示的就是常见的 BRDF 中的 $G_2$ 项):

In most of this paper we will use the uncorrelated form of the shadowing term written as a product of the two independent factors for each of the two directions:

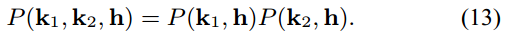
只有某些情况下采用了具有相关性的 $P(\bold k_1, \bold k_2, \bold h)$.

通过文章描述的推导, 最终可以获得下面的 BRDF 表达形式 $\rho(\bold k_1, \bold k_2)$, 其中 $\bold k_1$ 和 $\bold k_2$ 是入射和出射光线的方向向量.

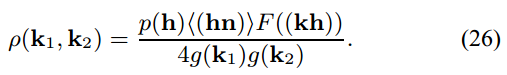
其中 $g(\bold k)$ 的表达式是:

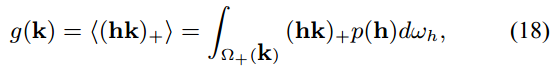
其表达的是法向量方向 $\bold h$ 在 $\bold k$ 方向的投影, 即 $\bold h \cdot \bold k$ 在正半球积分区域上的统计平均值, 其中的积分区域是如下图所示:

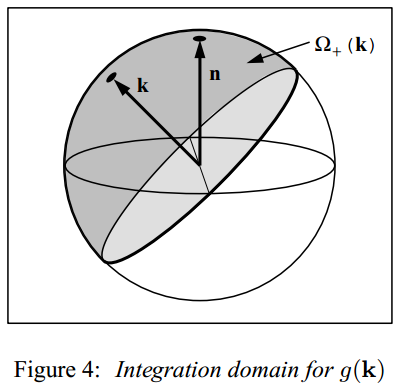
要计算 $g(\bold k)$, 通常需要使用基于数值或符号形式, 对关于 $p(\bold h)$ 的表达式进行积分. 对于大部分 $p(\bold h)$, 都无法获得解析的积分结果. 对于一般的情况, 特别是带有参数 (例如曲面粗糙度, 各向异性延展系数等等) 的情况, 可以使用 MATLAB 等数值计算工具进行计算后, 对积分结果进行拟合后, 用于实时渲染的 BRDF 公式中.

对假设条件的讨论

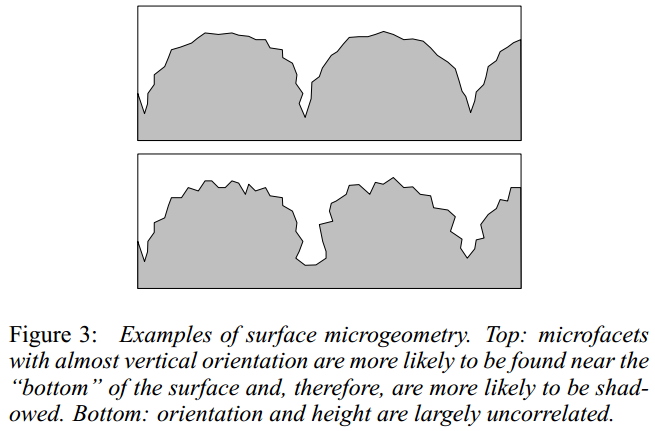
由于 $p(\bold h)$ 显然不能完全描述一个曲面, 曲面细节的遮挡关系, 曲面的几何细节也无法被 $p(\bold h)$ 所描述:

Note that surface description in the language of p(h) is less detailed than that of using height correlation functions.

The two surfaces in Figure 3 may still have the same distribution p(h) and there is no way for us to distinguish between the two cases. Similarly, we will not be able to distinguish, for example, between “positive” and “negative” cylinders of Poulin and Fournier [16] but from their images it is clear that the differences in appearance due to microfacet visibility issues and not to the distribution of microfacets are minor in this case.

作者这里引用的 Poulin 1990⁷ 中, 绘制了在同样的 $p(\bold h)$ 分布下, 两种相反的曲面形式 (Positive and Negative Cylinders) 的不同渲染效果.

可以看出 $p(\bold h)$ 无法描述遮挡关系导致的渲染差异, 但是注意到上述的结果没有仔细注意画面细节是看不到差异的. 这点作者也预料到了, 因此, 在本文中作者也简化了遮挡关系与阴影遮挡因子 $G$ 的计算. 这里可以简单地概括成, 本文的 $G$ 的计算没有细致地考虑表面的遮挡关系, 但是总体上该简化有明显的合理性.

方法应用

1. 原文中的重要应用

首先, 作者通过下面的, 带各向异性参数的高斯分布作为 $p(\bold h)$, 用来模型 Gaussian 分布的微表面形式, 这种形式的分布形式又常常被称作为 Beckmann 分布.

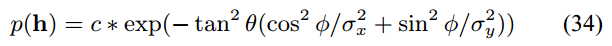
作者与和 Ward 1992² 的结果进行对比, 验证了通过该方法产生的 BRDF 可以达到和其相似的效果, 即可以正确表现各向异性的金属球.

绸缎 (Satin). 原文基于下图所示的模型进行绸缎材质 $p(\bold h)$ 的建模.

作者假设上述的绸缎材质的表面上由两种类型的部分组成. 微观上, 70% 的部分是平缓的部分, 30% 是弯曲的部分, 因此有表达式 $p(\bold h) = 0.7 * p_{flat}(\bold h) + 0.3 * p_{ends}(\bold h)$. 其中每一部分的分布都是用某个特定参数的高斯分布表示, 因此总体上, 这个分布是两个高斯分布的线性组合. 作者展示了结果, 右侧是我在网上随便找的一个真实的 Satin 图片, 可以看出他们的外观是很接近的.

丝绒 (Velvet). 原文基于某种观察 (这种说法在丝绒材质的文章中很常见, 一般认为丝绒材质的法向量有一个接近高斯倒数的分布), 将 $p(\bold h)$ 的建模为:

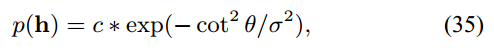
这个分布的计算结果如下图, 右侧的图是 Koenderink 2003³ 中一张丝绒照片. 可以看到左边的渲染结果和常见的丝绒还是有些差距 (虽然可以看出一些逆散射成分, 但是还是差了很多).

随后, 作者又引入了一些修正, 例如: 使用了有自相关性的遮挡因子, 引入了新的高斯分布成分等等. 渲染结果如下图, 可是还是可以看出这个效果仍然有塑料的痕迹. 同时, 由于采用了 Lambertian Diffuse, 下面右图右侧的边缘并不像真实的丝绒 (丝绒材质一般有很重要的 Asperity Scattering 的成分³).

特殊 BRDF

通过将 $p(\bold h)$ 调制上某些图像信号, 例如某些贴图, 就可能实现本文第一张图片的那样的定制高光.

2. 布料材质上的应用之一 Production Friendly Microfacet Sheen BRDF⁵

该文使用本文的方法, 同时对 $G_2$ 的计算进行了一定修正. (我个人推断) 通过使用的下面的积分公式⁴, 再通过函数拟合, 获得了一个相对简单的解析表达式.

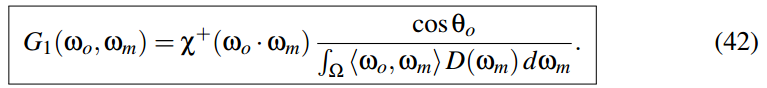
他们的丝绒材质渲染结果对比如下:

最后, 介绍下的丝绒 (Velvet) 材质的建模. 两篇文章都指向下面的描述 ^{1 5}:

We follow up on the approach of using cylindrical microfibers [Ashikmin et al. 2000] as the main source of scattering.

In their virtual gonioreflectometer, Westin et al. [27], model velvet microstructure as a forest of narrow cylinders (fibers) with the orientation of each cylinder perturbed randomly. While it is difficult to write an exact p(h) corresponding to such “surface” for the reasons outlined in Section 2, a simple intuitive form of this function written as an “inverse Gaussian” heightfield is enough to capture the main character of the distribution.

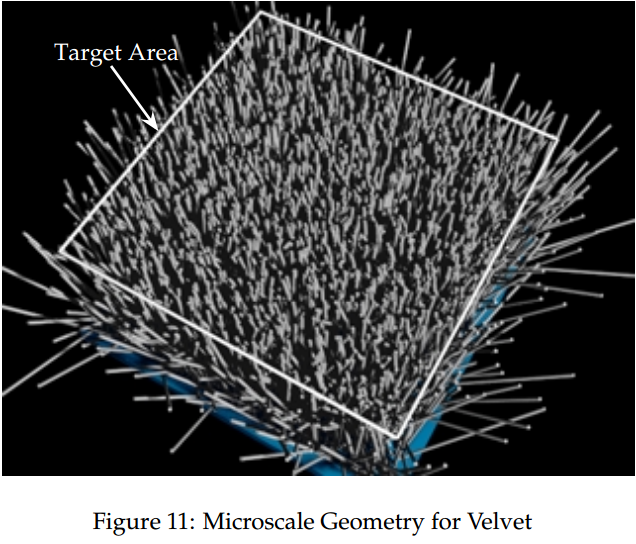
Westin 1992⁶ 通过射线追踪进行的渲染结果如下图.